次に外接正三角形の最大値、最小値を求めてみます。

三角形ABCで、AB=c、BC=a、CA=b、（a≧b≧c）

外接円の半径をRとします。

この三角形に外接する正三角形の1辺について考えてみます。

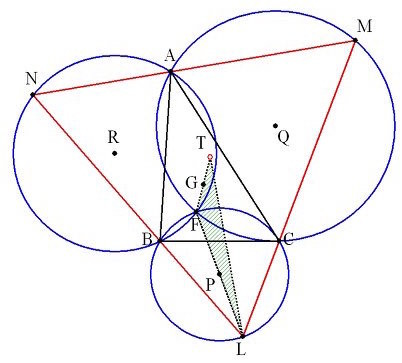
AB、BC、CAを弦とする円周角60°の円P、Q、Rをかきます。

半径は、それぞれ、c/√3、a/√3、b/√3、

3円の交点をGとします。（1点でまじわる。フェルマー点）

頂点ABCを通る正三角形DEFの頂点は、この3つの円周上にあります。

外接正三角形の最大値

この正三角形の1辺の最大値は、GDがもっとも長いとき、

すなわちGPDが直径のとき。(赤い三角形 )

この長さの二乗は、

△GPDBEQで、DG=2c/√3、EG=2a/√3

また、∠GBA=∠GDA、∠GBC=∠GECより

∠DGE=180°-(60°-∠GDA)-(∠60°-∠GEC)=60°+(∠GBA+∠GBC)=60°+∠B

余弦定理より、

DE²=DG²+EG²-2DG・EGcos(60°+B)

cosB=(a²+c²-b²)/2ac、sinB=b/2Rをつかって、

DE²=2(a²+b²+c²)/3+2√3abc/3R

ちなみに、これはナポレオンの正三角形PQRの1辺の2倍である。

外接正三角形の最小値

最小値は、GDがもっとも短いとき。

(1)∠Aだけが60°以上のとき

GDの最小値は、DがBにかさなるとき（GBが最小）（青い三角形）

（証明は下に※２）

このときのFの位置をL、Eの位置をMとすると、

△ALCで、正弦定理より、

AC/sin∠ALC=AL/sin∠ACLより、b/(√3/2)=AL/sin(A-60°)

AL=2bsin(A-60°)/√3

cosA=(b²+c²-a²)/2bc、sinA=a/2Rをつかって、

AL=ab/2√3R-(b²+c²-a²)/2c

よって、

BL=BA+AL=c+AL=√3ab/6R+(a²+c²-b²)/2c

(2)∠Aが120°以上のとき

CAと円Pの交点をNとする。

Gは△ABCの外部にあるので、GDの最小値は、DがNにかさなるとき

求め方は(1)と同じ

CN=√3ac/6R+(a²+b²-c²)/2b

 (3)二つの内角が60°以上のとき

図のように、ABを通る正三角形をCLL'、CBを通る正三角形をCP'P、

CAを通る正三角形をCNN'とする。

・CN>CPの証明（緑の正三角形と青の正三角形）

∠CNP=∠CBA、∠CPN=∠CAB

∠CAB>∠CBAより、∠CPN>∠CNP

よって、CN>CP(青の正三角形の方が小さい)

・CLとCPの大小（青の正三角形と赤の正三角形）

∠CP'L=∠CAB=A

∠CLP'=∠CAP'=C+60°=240°-(A+B)

∠CLP'-∠CP'L=240°-(2A+B)

よって、

2A+B≦240°のとき、

∠CLP'≧∠CP'L

すなわち、CP'≧CL(青い正三角形が最小)

最小値CL=2b/√3・sinA=ab/(√3R)

2A+B>240°のとき、

∠CLP'<∠CP'L

すなわち、CP'<CL（赤い正三角形が最小）

最小値CP'=2b/√3・sin(C+60°)=bc/(2√3R)+(a²+b²-c²)/2a

以上のことから、x軸をA、y軸をBの座標平面上に最小の正三角形の領域を

色分けすると、次のようになる。

赤…ABを通る正三角形を最小とするとき。

青…BCを通る正三角形を最小とするとき。

緑…CAを通る正三角形を最小とするとき。

※1必要ならば、R=abc/√{(a+b+c)(b+c-a)(a+c-b)(a+b-c)}をつかってもよい。

※2[証明]

CAと円Pの交点をNとする。

△ACL∽△ABN

AC=kAB、AL=kAN（円Rの方が円Pより大きいので、k≧1）

LB=AL+AB=kAN+AB、CN=AC+AN=kAB+AN

よって、

LB-CN=(k-1)(AN-AB)

(1)A≧120°のとき、

∠ANB≦∠ABNより、AB≦AN

CN≦LB（緑の正三角形が最小）

(2)A<120°のとき、

∠ANB>∠ABNより、AB>AN

LB<CN（青の正三角形が最小）