(オイラー線に垂直な直線)

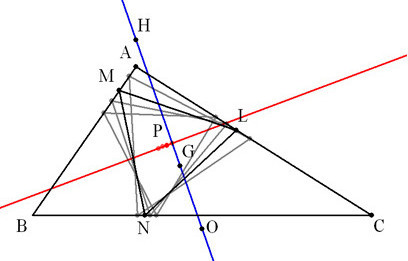
 [KONDOの定理]　内接正三角形の重心の軌跡　

三角形の三辺上（またはその延長上）に頂点をもつ正三角形の重心は、

その三角形のオイラー線に垂直な直線上にある。

この直線の三線座標による方程式は、

  {p(A,B,C)+p(A,C,B)}x+{p(B,A,C)+p(B,C,A)}y+{p(C,A,B)+p(C,B,A)}z=0

 ただし、p(a,b,c)=(2sinasinb+√3sinc)sin(c-a)

［証明］

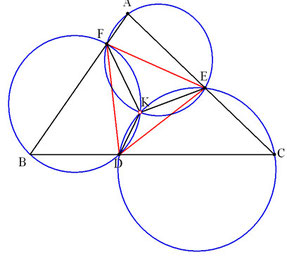
△DEFを△ABCに内接する正三角形とします。

△AEFと△BFDの外接円の交点をKとします。

∠EKD=∠A+∠Bだから、

∠EKD+∠C=180°

よって、△CDEの外接円もKを通る。

[定理1]

△AEF、△BFD、△CDEの外接円は、1点Kで交わる。

∠BAK=∠FEK、∠DCK=∠DEK、∠FEK+∠DEK=60°より、

∠AKC=∠B+∠BAK+∠BCK=∠B+60°で一定

同様に∠BKA=∠C+60°、∠CKB=∠A+60°で一定であるから、

点Kは定点である。

さらに、∠EKF=180°-∠A、∠BAK=∠FEKで一定であるので、

△EKF等は、相似に動く。

[定理2]　等力点の性質

△AEF、△BFD、△CDEの外接円の交点Kは定点であり、

∠AKC=∠B+60°、∠BKA=∠C+60°、∠CKB=∠A+60°

△EKF、△FKD、△DKEは、相似に動く。

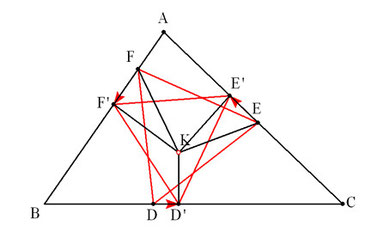
ここで、△D'E'F'を△ABCに内接する別の正三角形とします。

BD'=x、CE'=y、AF'=z、KD'=kd、KE'=ke、KF'=kf、D'E'=E'F'=F'D'=kg

BK=l、CK=m、AK=nとかくと、(kは相似比)

内接四角形BDKFで、トレミーの定理より、

BD・KF+KD・BF=BK・DFから

kfx+kd(c-z)=klg

よって、

dz=fx+cd-lg

同様にして、

fy=ez+bf-ng、ex=dy+ae-mg

したがって、xがd増加すると、yはe、zはf増加するので、

DD'：EE'：FF'=d：e：f

[定理3]

△DEF、△D'E'F'が△ABCに内接する正三角形とするとき、

DD'：EE'：FF'=d：e：f（一定）である。

ここで、△DEFの重心G、△D'E'F'の重心をG'を考えると、

G↑=(D↑+E↑+F↑)/3

G'↑=(D↑+DD'↑+E↑+EE'↑+F↑+FF'↑)/3=G↑+BC↑/|BC↑|×kd+CA↑/|CA↑|×ke+AB↑/|AB|×kf

=G↑+k(BC↑/|BC↑|×d+CA↑/|CA↑|×e+AB↑/|AB|×f

となり、

GG'=k(BC↑/|BC↑|×d+CA↑/|CA↑|×e+AB↑/|AB|×fは一定方向であり、

重心はの1つの直線上にある。

[定理4]　重心の軌跡

△ABCに内接する正三角形の重心は、1つの直線上にある。

D'、E'、F'がKからの垂線の足の場合で計算します。

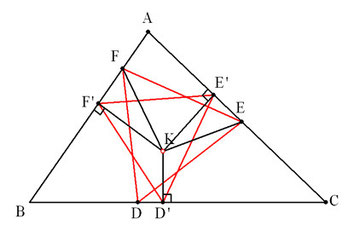
△EKF∽△E'K'F'で、EK>E'Kより、EF>E'F'から、

正三角形D'E'F'は、内接する正三角形で最小の三角形になります。

[定理5]　最小の三角形

内接する最小の正三角形は、定点Kからの垂足三角形である。

外接円AF'KE'、F'BD'K、E'KD'Cの半径を、R1、R2、R3とします。

正弦定理より、(R=△ABCの外接円の半径)

E'F'=2R2sinA、F'D'=2R1sinB、D'E'=2R3sinC

E'F'=F'D'=D'E'より、

R1sinA=R2sinB=R3sinC

よって、

R1：R2：R3=1/sinA：1/sinB：1/sinC

正弦定理より、

=1/a：1/b：1：c

[定理6] 　頂点からの距離の比

AK：BK：CK=1/sinA：1/sinB：1/sinC=1/a：1/b：1/c

∠KBF'=∠KD'F'、∠KCE'=∠KD'E'、∠F'D'E'=∠KD'F'+∠KD'E'=60°より

∠BKC=∠KBF'+∠KCE'+∠BAC=∠KD'F'+∠KD'E'+∠A=∠A+60°

同様に、∠CKA=∠B+60°、∠AKB=∠C+60°

よって、

△KBC=1/2・BC・KD'=1/2・a・KD'=1/2・KB・KC・sin∠BKC

=1/2・2R2・2R3・sin(A+60°)から、

KD'=4(R2・R3)/a・sin(A+60°)

同様にして、KE'=4(R3・R1)/b・sin(B+60°)、KF'=4(R1・R2)/c・sin(C+60°)

よって、

KD'：KE'：KF'=sin(A+60°)/aR1：sin(B+60°)/bR2：sin(C+60°)/cR3

定理6と正弦定理より、

KD'：KE'：KF'=sin(A+60°)：sin(B+60°)：sin(C+60°)

[定理7]　等力点の三線座標

KD'：KE'：KF'=sin(A+60°)：sin(B+60°)：sin(C+60°)

（定点Kの三線座標）

△ABCの外心Oから、BC、CA、ABへの垂線の足を、G、I、J、垂心をHとします。

新ためて、任意の点Pから、BC、CA、ABへの垂線の足を、D、E、F、とします。

OG=OBcos∠BOG=RcosA 等より、

OG：OI：OJ=cosA：cosB：cosC (外心Oの三線座標)

オイラー線の方向ベクトルは、

OH↑=OA↑+OB↑+OC↑

今、PD↑+PE↑+PF↑が、オイラー線と同じ方向のベクトルだとすると、

PD↑⊥BC↑等により、

|PD|×BC↑/|BC|+|PE|×CA↑/|CA|+|PF|×AB↑/|AB|、(PV↑とする)

は、オイラー線に垂直なベクトル

BC↑=OC↑-OB↑、CA↑=OA↑-OC↑、AB↑=OB↑-OA↑より、

|PD|=x、|PE|=y、|PF|=z、とかくと、

PV↑

=y/b(OA↑-OC↑)+z/c(OB↑-OA↑)+x/a(OC↑-OB↑)

=(y/b-z/c)OA↑+(z/c-x/a)OB↑+(x/a-y/b)OC↑

したがって、(OA↑・OA↑)=R²等、(OB↑・OC↑)=(OB²+OC²-BC²)/2=(2R²-a²)/2等を使って、

(OH↑・PV↑)

=(c²-b²)x/2a＋（a²-c²)y/2b+(b²-a²)z/2c

OH↑⊥PV↑より、(OH↑・PV↑)=0から、

(c²-b²)x/a＋(a²-c²)y/b+(b²-a²)z/c=0

bc(c²-b²)x＋ac(a²-c²)y+ab(b²-a²)z=0

これが、PD↑+PE↑+PF↑が、オイラー線と同じ方向になる点Pの三線座標による方程式となります。

［定理8］

PD↑+PE↑+PF↑が、オイラー線と同じ方向になる点Pの

三線座標による方程式

bc(c²-b²)x＋ac(a²-c²)y+ab(b²-a²)z=0

疑似重心(ルモアーヌ点)の三線座標、（a、b、c)

外心の三線座標、(cosA、cosB、cosC)=(a(b²+c²-a²)、b(c²+a²-b²)、c(a²+b²-c²)

はこの方程式を満たす。

また、

［定理7］の正三角形の定点K　　(sin(A+60°)、sin(B+60°)、sin(C+60°))

は、sin(A+60°)=sinAcos60°+cosAsin60°=a/4R+√3/2・(b²+c²-a²)/2bc等より、

この方程式を満たす。

このことから、点(sin(A+θ)、sin(B+θ)、sin(C+θ))

もこの方程式を満たすことにきづく。

θ=0のとき、疑似重心(ルモアーヌ点)、θ=90°のとき、外心である。

x=sin(A+θ)、y=sin(B+θ)、z=sin(C+θ)は、この直線のパラメータ表示であり、

この3式からθを消去すると、

sin(B-C)x+sin(C-A)y+sin(A-B)z=0

がえられる。

［定理9］ブロカール軸

疑似重心、外心をむすぶ直線の三線座標による方程式は、

bc(c²-b²)x＋ac(a²-c²)y+ab(b²-a²)z=0

または、

sin(B-C)x+sin(C-A)y+sin(A-B)z=0

［定理10］

三角形に内接する正三角形の定点K（等力点）は、疑似重心、外心を結ぶ直線上にある。

以上のことから、内接する正三角形の重心にもどり考えると、

(BC↑/|BC↑|×d+CA↑/|CA↑|×e+AB↑/|AB|×f

//(BC↑/|BC↑|×sin(A+60°)+CA↑/|CA↑|×sin(B+60°)+AB↑/|AB|×sin(C+60°)

は、オイラー線に垂直な方向ベクトルであることがわかる。

重心の三線座標は、

（2sin(A+60°)+sin(B+60°)cosC+sin(C+60°)cosB、2sin(B+60°)+sin(C+60°)cosA+sin(A+60°)cosC、2sin(C+60°)+sin(A+60°)cosB+sin(B+60°)cosA）

=√3/2・(2sinBsinC+√3sinA、2sinCsinA+√3sinB、2sinAsinB+√3sinC）

GG'↑の方向は、

(sin(B+60°)sinC-sin(C+60°)sinB、sin(C+60°)sinA-sin(A+60°)sinC、sin(A+60°)sinB-sin(B+60°)sinA）

=-√3/2・(sin(B-C)、sin(C-A)、sin(A-B))

x、y、zがその直線上にあるためには、

行列式=0

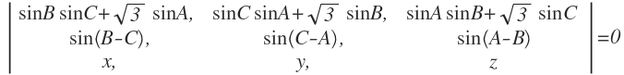
この直線の三線座標による方程式は、

{(2sinCsinA+√3sinB)sin(A-B)-(2sinAsinB+√3sinC)sin(C-A)}x

+{(2sinAsinB+√3sinC)sin(B-C)-(2sinBsinC+√3sinA)sin(A-B)}y

+{(2sinBsinC+√3sinA)sin(C-A)-(2sinCsinA+√3sinB)sin(B-C)}z

=0

p(a,b,c)=(2sinasinb+√3sinc)sin(c-a)とすると、

 {p(A,B,C)+p(A,C,B)}x+{p(B,A,C)+p(B,C,A)}y+{p(C,A,B)+p(C,B,A)}z=0

(なお、正三角形のオイラー線はなく、点になるので、

軌跡も点になる。)

よって、KONDOの定理が証明された。

[別解]

BC↑、CA↑、AB↑、の単位ベクトルは、それぞれ、(1、0)、(-cosC、sinC)、(-cosB、-sinB)

それぞれに垂直な、OG↑、OI↑、OJ↑、の単位ベクトルは、それぞれ、

(0、-1)、(sinC、cosC)、(-sinB、cosB)

よって、

オイラー線の方向ベクトルは、

OH↑=OA↑+OB↑+OC↑=1/2・(OB↑+OC↑)+1/2・(OA↑+OC↑)+1/2・(OA↑+OB↑)

=OG↑+OI↑+OJ↑

=k1cosA(0、-1)+k1cosB(sinC、cosC)+k1cosC(-sinB、cosB)

　(k1は定数）

=k1(sin(C-B)、2cosBcosC-cosA)

KV↑=(BC↑/|BC↑|×k2sin(A+60°)+CA↑/|CA↑|×k2sin(B+60°)+AB↑/|AB|×k2sin(C+60°)(k2は定数）

=k2sin(A+60°)(1、0)+k2sin(B+60°)(-cosC、sinC)+k2sin(C+60°)(-cosB、-sinB)

=√3/2・k2(cosA-2cosBcosC、sin(C-B)

よって、KV↑は、オイラー線に垂直である。